Introduction to Graphs

CS 351: Analysis of Algorithms

Author
Affiliation

Lucas P. Cordova, Ph.D.

Willamette University

Abstract

This lecture covers the introduction to graphs, including their definition, types, and applications. We will explore the different types of graphs, their properties, and their applications.

Executive Summary

TipWhat We’ll Discuss This Week
  • Introduction to graphs
  • Definition of graphs
  • Types of graphs
  • Applications of graphs

Introduction to Graphs

What Are Graphs?

When you hear “graph,” you might think of x-y plots, but in computer science, graphs represent relationships between objects.

Key Insight: Graphs model pairwise relationships between objects

Two Types of “Graphs”

Mathematical Plot

  • x-axis and y-axis
  • Functions: f(n) = n, f(n) = log n
  • Continuous relationships

Graph Data Structure

  • Vertices (nodes) = objects
  • Edges = relationships
  • Discrete connections

Graph Fundamentals

Essential Vocabulary

Vertices (or Nodes):

  • The objects being represented
  • Examples: people, intersections, web pages

Edges:

  • The pairwise relationships
  • Examples: friendships, roads, hyperlinks

Notation: G = (V, E) where V = vertices, E = edges

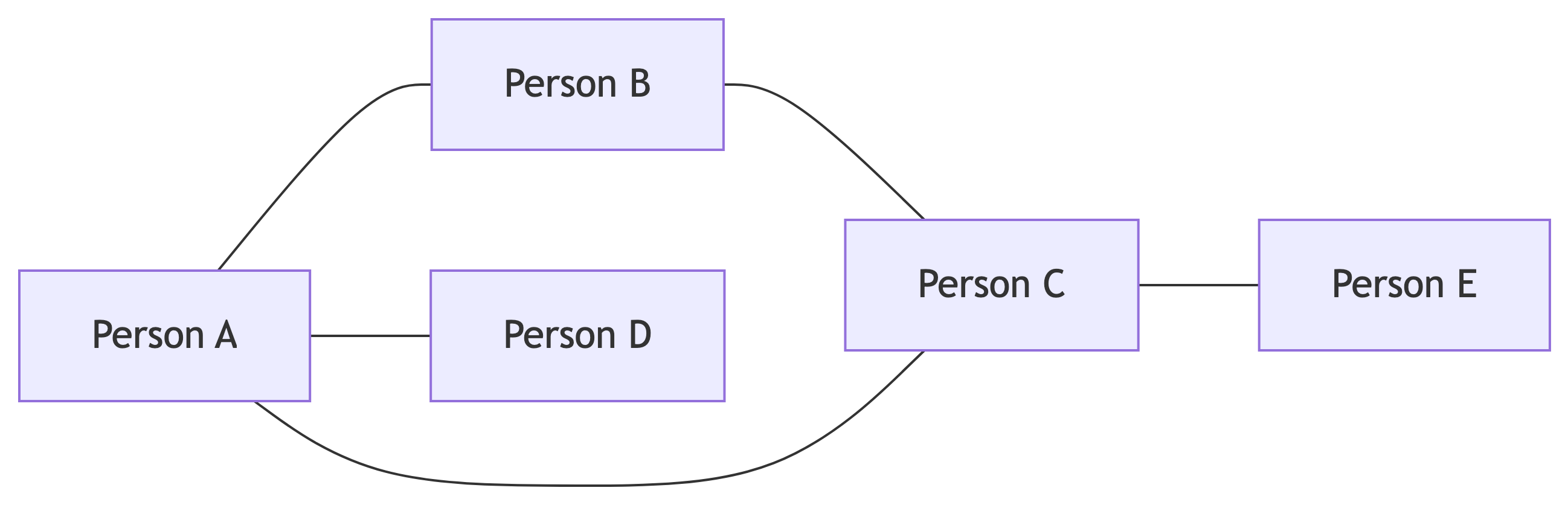
Directed vs Undirected Graphs

Undirected Graph

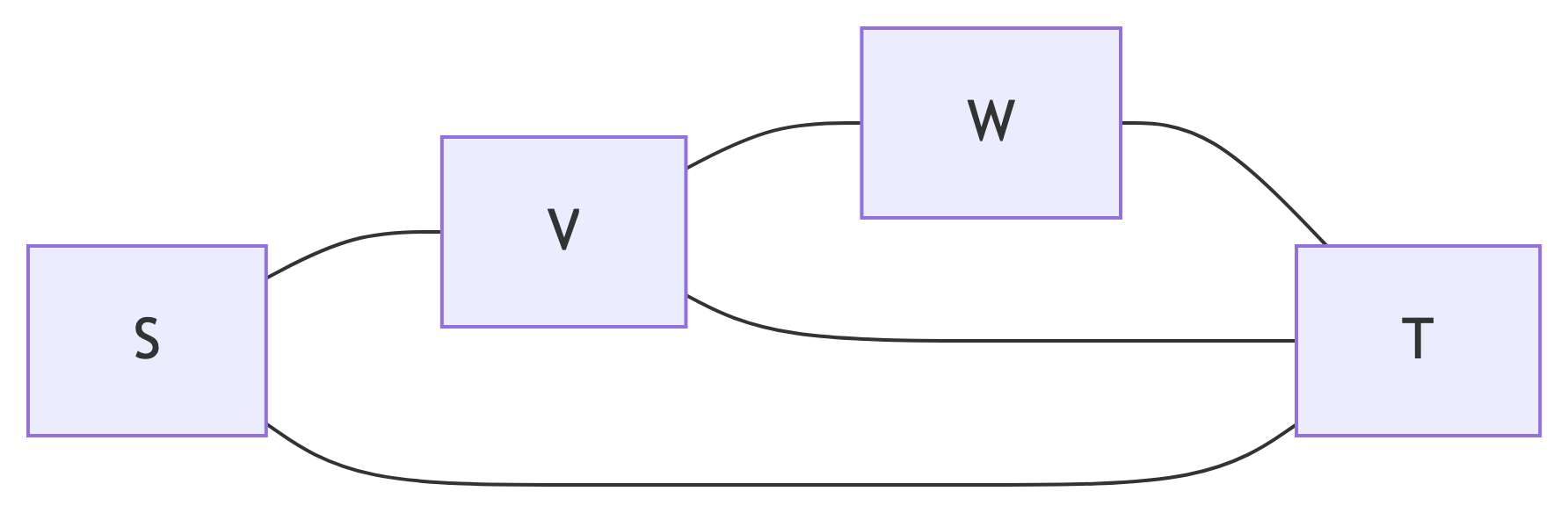
  • Edges are unordered pairs {v, w}
  • No direction matters
  • (v, w) = (w, v)

Directed Graph

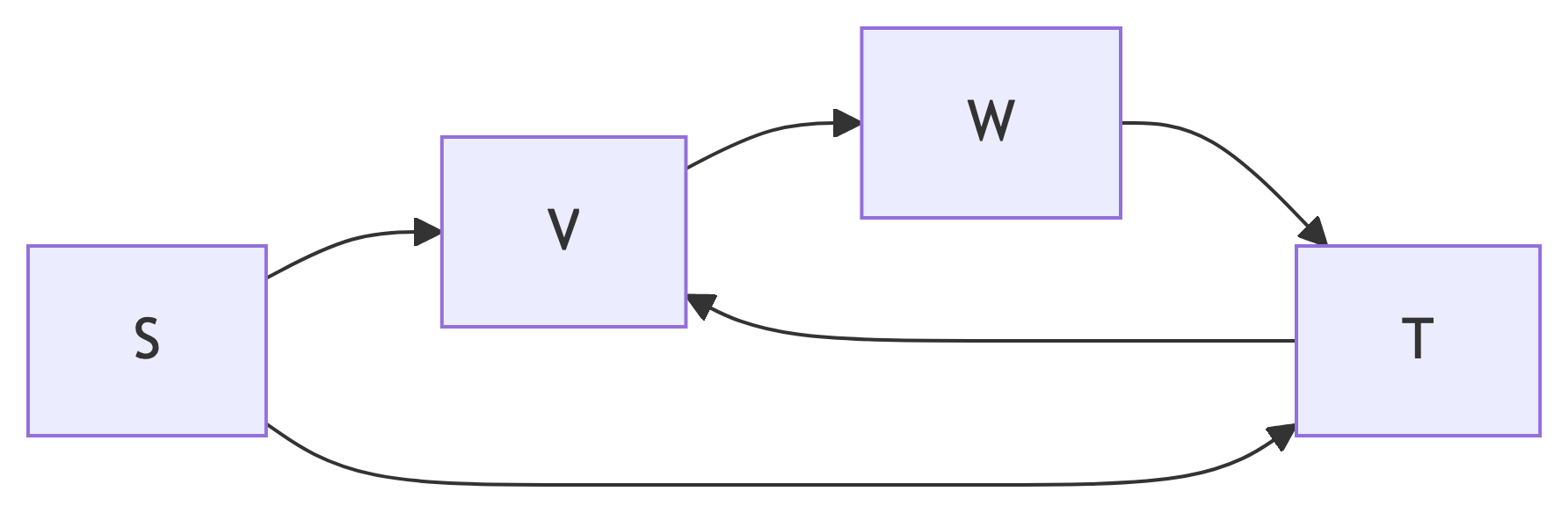
  • Edges are ordered pairs (v, w)
  • Direction matters: v → w
  • v = tail, w = head

Graph Notation Deep Dive

For any graph G = (V, E):

  • |V| = n (number of vertices)
  • |E| = m (number of edges)
  • Vertices often labeled: v₁, v₂, …, vₙ
  • Edges connect vertex pairs

Example: Social network graph

  • V = {Alice, Bob, Carol, Dave}
  • E = {(Alice,Bob), (Bob,Carol), (Alice,Carol)}

Real-World Applications

Road Networks

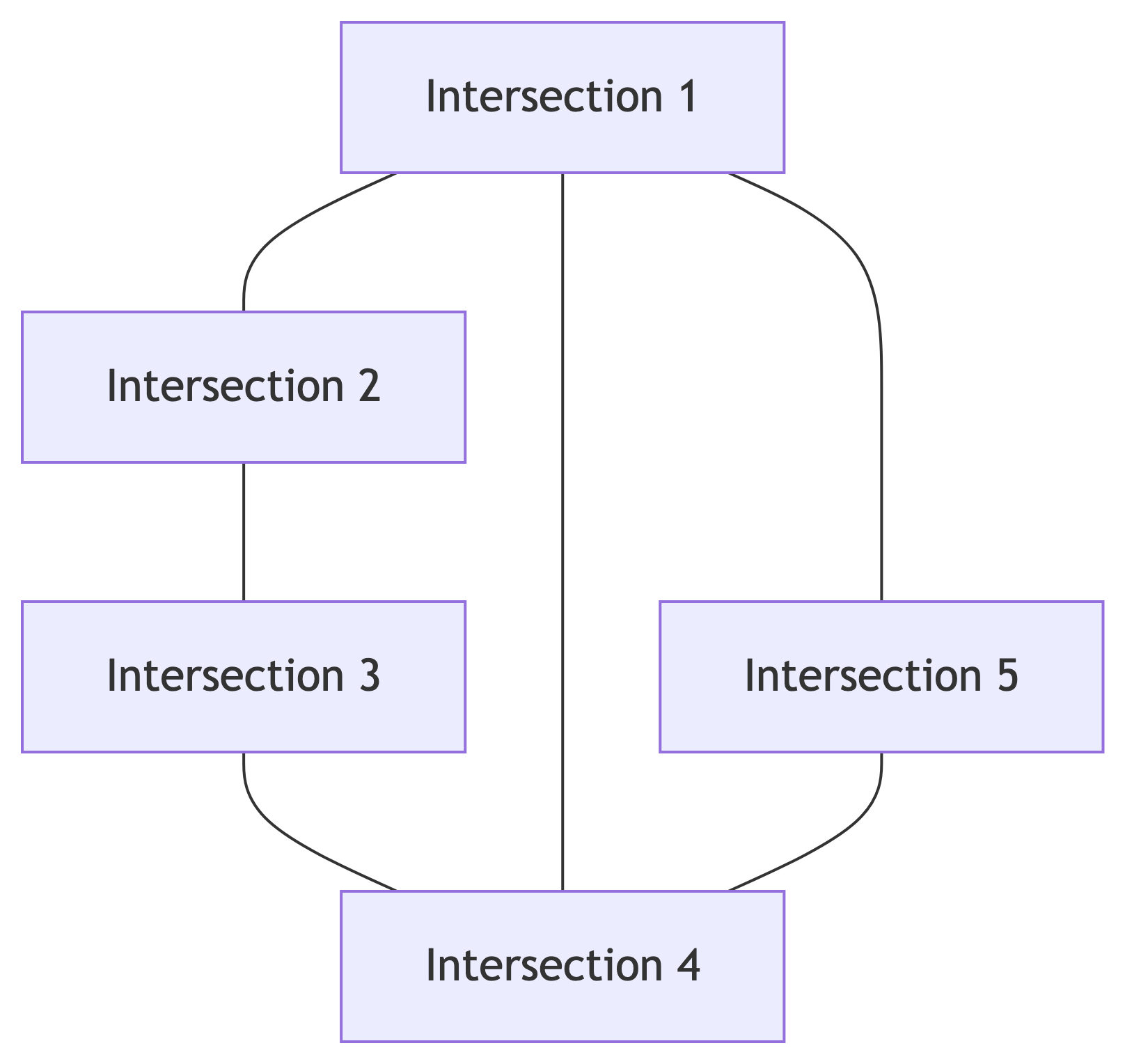
Implementation:

  • Vertices = intersections
  • Edges = road segments
  • Used by GPS navigation systems

Social Networks

Applications:

  • Friend recommendations
  • Information spread analysis
  • Community detection

Web Structure

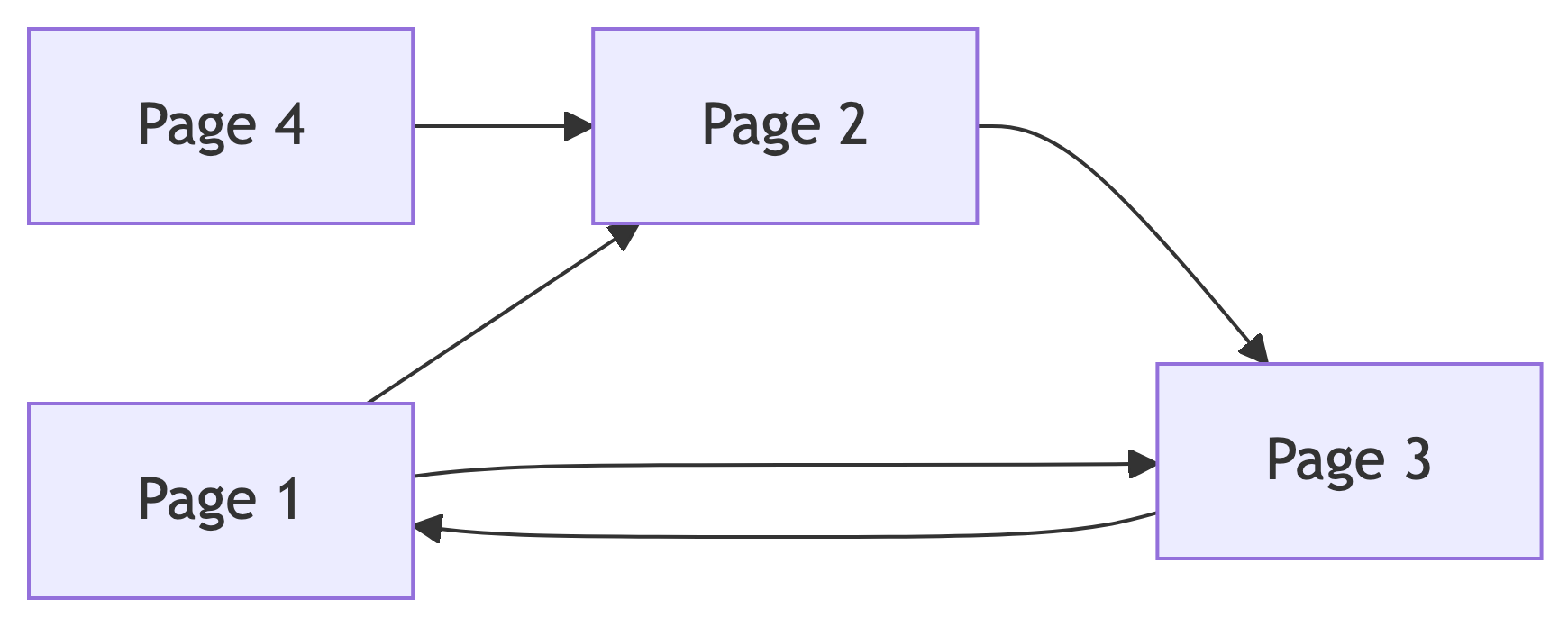
Key Features:

  • Vertices = web pages
  • Edges = hyperlinks
  • Foundation of PageRank algorithm

Dependency Networks

Use Cases:

  • Project scheduling
  • Software compilation
  • Course prerequisites

Graph Size Analysis

Measuring Graph Size

Two key metrics:

  • n = number of vertices
  • m = number of edges

Fundamental bounds:

  • Minimum edges: m ≥ 0
  • Maximum edges (undirected): m ≤ n(n-1)/2
  • Maximum edges (directed): m ≤ n(n-1)

Sparse vs Dense Graphs

Sparse Graph: m ≈ O(n)

Dense Graph: m ≈ O(n²)

When Is a Graph Dense?

Mathematical Definition:

  • Sparse: m = O(n) or m = O(n log n)
  • Dense: m = Θ(n²)

Practical Examples:

  • Social networks: typically sparse
  • Complete graphs: always dense
  • Road networks: usually sparse

Graph Representation

Two Main Approaches

Adjacency Lists:

  • Space efficient for sparse graphs
  • Fast edge iteration
  • Preferred for most algorithms

Adjacency Matrix:

  • Space efficient for dense graphs
  • Fast edge lookup
  • Simple implementation

Adjacency List Representation

Core Components:

  1. Vertex Array: stores vertex information
  2. Edge Array: stores edge information
  3. Edge → Vertex pointers: each edge points to endpoints
  4. Vertex → Edge pointers: each vertex points to incident edges

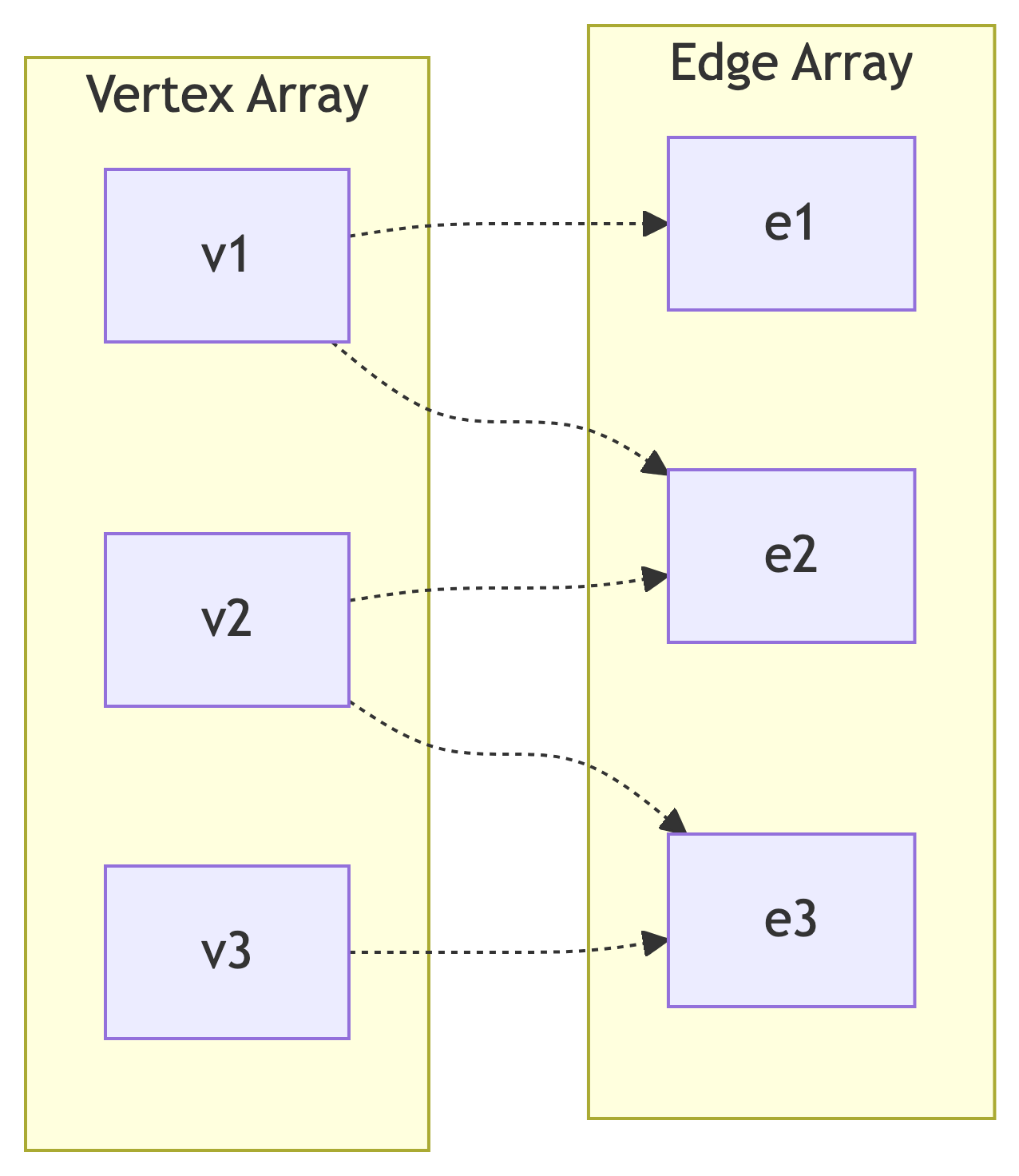
Adjacency List: Space Analysis

Space Complexity: Θ(m + n)

Breakdown:

  • Vertex array: Θ(n)
  • Edge array: Θ(m)
  • Edge→vertex pointers: Θ(m)
  • Vertex→edge pointers: Θ(m)

Total: Θ(n + m + m + m) = Θ(m + n)

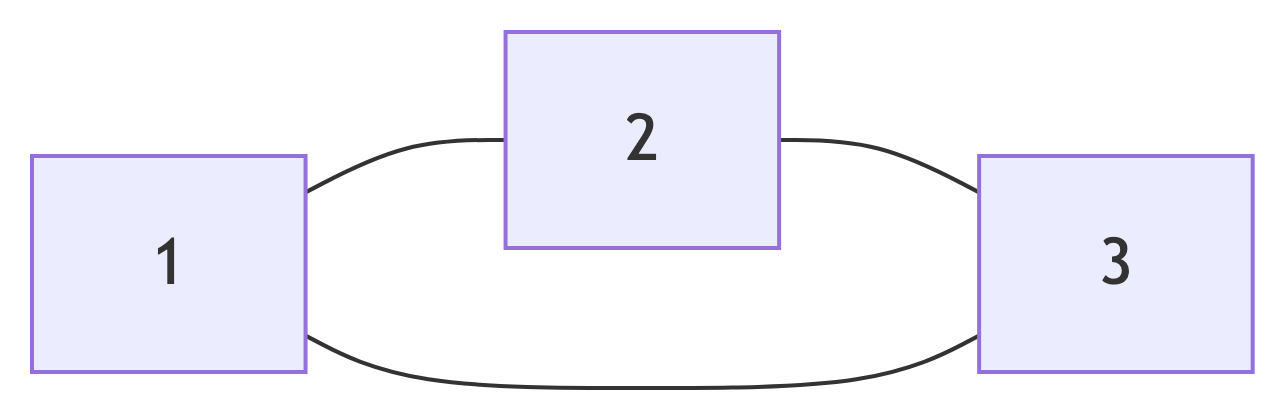
Adjacency List Example

Graph:

Adjacency List Representation:

  • Vertex 1: [2, 3]
  • Vertex 2: [1, 3]
  • Vertex 3: [1, 2]

Each vertex stores list of neighbors

Adjacency Matrix Representation

Structure: n × n matrix A where:

  • A[i,j] = 1 if edge (i,j) exists
  • A[i,j] = 0 if no edge

Undirected graphs: A[i,j] = A[j,i] (symmetric)

Directed graphs: A[i,j] ≠ A[j,i] generally

Adjacency Matrix Example

Graph:

Matrix Representation:

    1  2  3
1 [ 0  1  1 ]
2 [ 1  0  1 ]
3 [ 1  1  0 ]

Adjacency Matrix: Space Analysis

Space Complexity: Θ(n²)

Characteristics:

  • Always uses n² bits regardless of edge count
  • Efficient for dense graphs (m ≈ n²)
  • Wasteful for sparse graphs (m ≈ n)
  • Fast edge existence queries: O(1)

Comparison and Trade-offs

Adjacency Lists vs Adjacency Matrix

Operation Adjacency List Adjacency Matrix
Space Θ(m + n) Θ(n²)
Edge lookup O(degree(v)) O(1)
Add edge O(1) O(1)
Remove edge O(degree(v)) O(1)
Find neighbors O(degree(v)) O(n)

When to Use Each Representation

Use Adjacency Lists when:

  • Graph is sparse (m ≈ n)
  • Need to iterate over neighbors frequently
  • Memory is limited
  • Most graph algorithms prefer this

Use Adjacency Matrix when:

  • Graph is dense (m ≈ n²)
  • Need fast edge existence queries
  • Working with mathematical graph operations
  • Graph size is small and fixed

Implementation Considerations

Adjacency Lists:

  • Dynamic arrays or linked lists
  • Easy to add/remove vertices
  • Cache-friendly for sparse graphs
  • Standard choice for most algorithms

Adjacency Matrix:

  • Fixed-size 2D array
  • Simple bit operations
  • Good for mathematical computations
  • Parallel processing friendly

Quiz Time!

Quiz Question 1

For an undirected graph with n vertices, what is the maximum possible number of edges?

  1. n
  2. n - 1
  3. n(n-1)/2
  4. n²

Quiz Question 2

Which representation is better for a sparse graph with 1000 vertices and 1500 edges?

  1. Adjacency Matrix
  2. Adjacency List
  3. Both are equivalent
  4. Depends on the operations

Quiz Question 3

In an adjacency list representation, how many operations are needed to check if edge (u,v) exists?

  1. O(1)
  2. O(log n)
  3. O(degree(u))
  4. O(n)

Practical Applications

Algorithm Performance Impact

Graph Search Algorithms:

  • Breadth-First Search: O(m + n)
  • Depth-First Search: O(m + n)
  • Both prefer adjacency lists

Shortest Path Algorithms:

  • Dijkstra’s: O((m + n) log n) with heaps
  • Works with both representations
  • Adjacency lists usually faster

Memory Usage in Practice

Real-world example: Facebook social graph

  • ~3 billion users (vertices)
  • ~200 billion friendships (edges)
  • Average degree: ~130
  • Adjacency matrix: 9 × 10¹⁸ bits ≈ 1 exabyte
  • Adjacency list: ~400 billion entries ≈ 1.6 TB

Clear winner: Adjacency lists!

Graph Processing Libraries

Common implementations:

  • NetworkX (Python): adjacency lists
  • igraph (R/Python): adjacency lists
  • GraphX (Spark): distributed adjacency lists
  • SNAP (C++): adjacency lists

Industry standard: Adjacency lists with optimizations

Advanced Topics Preview

What’s Next?

Graph Search Algorithms (Chapter 8):

  • Breadth-First Search (BFS)
  • Depth-First Search (DFS)
  • Connected Components
  • Topological Sort

Shortest Path Algorithms (Chapter 9):

  • Dijkstra’s Algorithm
  • Single-source shortest paths
  • Applications to routing

Graph Algorithm Complexity

All upcoming algorithms are “for-free primitives”:

  • Running time: O(m + n)
  • Just slightly more than reading input
  • Can apply liberally to understand graph structure

Key insight: Linear-time graph algorithms are incredibly powerful!

Modern Graph Challenges

Big Data Graphs:

  • Distributed storage and computation
  • Streaming graph algorithms
  • Approximate algorithms for massive graphs

Machine Learning on Graphs:

  • Graph Neural Networks
  • Node embeddings
  • Graph classification

Summary

Key Takeaways

Graph Fundamentals:

  • Graphs model pairwise relationships
  • Directed vs undirected matters
  • Vertices = objects, Edges = relationships

Representation Trade-offs:

  • Adjacency lists: Θ(m + n) space, prefer for sparse graphs
  • Adjacency matrix: Θ(n²) space, prefer for dense graphs
  • Most algorithms use adjacency lists

Design Principles

When designing with graphs:

  1. Identify vertices and edges clearly
  2. Choose representation based on density
  3. Consider the operations you’ll need most
  4. Remember adjacency lists are usually best
  5. Think about scalability early

Next Steps

Build on this foundation:

  • Practice implementing both representations
  • Study graph search algorithms
  • Explore real-world graph datasets
  • Consider distributed graph processing
  • Learn graph visualization techniques