Analytic Combinatorics
CS 351: Analysis of Algorithms
Learning Objectives
- Define analytic combinatorics.
- Recall complexity classifications.
- Distinguish between Big-O, Big-Omega, Big-Theta.
- Discuss issues with Big-O notation.
- Apply scientific method to analyze algorithms.
Introduction to Analytic Combinatorics
Analysis of Algorithms
Charles Babbage 1840
“As soon as an Analytics Engine exists, it will necessarily guide the future course of science. Whenever any result is sought by its aid, the question will arise - By what course of calculation can these results be arrived at by the machine in the shortest time?”
Analytical Engine

Analysis of Algorithms
Ada Lovelace 1860
First computer program to calculate the Bernoulli numbers using the analytical engine.
Ada Lovelace - First Programmer

Recalling Big-O
Definition: Big-O notation describes the upper bound (worst case) of the time complexity (speed) or space complexity (storage) of an algorithm.
Purpose: Helps predict how an algorithm will perform as the input size grows.
Use Case: Essential in computer science for comparing the efficiency of algorithms.
Why are we focused on time and space so much? 👀
Time and Space Complexity
- Time Complexity: Measures how the runtime of an algorithm changes relative to the input size.
- Space Complexity: Measures how the amount of memory needed by an algorithm changes with input size.
Big-O Complexity Classes
| Notation | Name | Description |
|---|---|---|
| \(O(1)\) | Constant Time | Execution remains constant regardless of input size |
| \(O(\log n)\) | Logarithmic Time | Execution time increases logarithmically |
| \(O(n)\) | Linear Time | Execution time increases linearly |
| \(O(n\log n)\) | Linearithmic Time | Execution time increases linearly and logarithmically combined |
| \(O(n^2)\) | Quadratic Time | Execution time increases quadratically |
| \(O(n^3)\) | Cubic Time | Execution time increases cubically |
| \(O(2^n)\) | Exponential Time | Execution time doubles with each additional element |
| \(O(n!)\) | Factorial Time | Execution time increases factorially |
Problems with Big-O
Example: Two sorting algorithms
Quicksort
- Worst-case number of compares: \(O(n^2)\)
- Classification: \(O(n^2)\)
Mergesort
- Worst-case number of compares: \(O(n\log n)\)
- Classification: \(O(n\log n)\)
BUT… ACTUALLY!
Quicksort is actually twice as fast as Mergesort and uses half the space.
Theory of Algorithms
Other Notations - Formal Definitions
- “Big-O” for upper bounds
- \(g(N) = O(f(N)) \iff |g(N)/f(N)|\) is bounded from above as \(N \to \infty\)
- Worst case
- “Big-Omega” for lower bounds
- \(g(N) = \Omega(f(N)) \iff |g(N)/f(N)|\) is bounded from below as \(N \to \infty\)
- Best case
- “Big-Theta” for order of growth
- \(g(N) = \Theta(f(N)) \iff O(f(N))\) and \(g(N) = \Omega(f(N))\)
- Exact (“within a constant factor”)
Big-O Limitations
- Pessimistic View: Big O primarily describes worst-case performance
- Not Always Representative: Many algorithms rarely encounter worst-case scenarios
- Overemphasis on Asymptotic Behavior: May not be relevant for moderate input sizes
Big-Omega Limitations
- Overly Optimistic: Describes best-case performance which rarely occurs
- Rarely Applicable: Most real-world problems don’t operate under best-case conditions
Big-Theta Limitations
- Ignores Variability: Indicates growth rate in both best and worst cases
- Rarely Applicable: By averaging performance, critical nuances might be obscured
Analysis of Algorithms
Current State of the Art
Traditional approach: > Analyze worst case scenario and use Big-O notation for the upper bound.
But…
Don’t despair!
WE CAN DO BETTER!
Analysis of Algorithms
Don Knuth 1960
To analyze an algorithm:
- Develop a good implementation.
- Identify unknown quantities representing the basic operation.
- Determine the cost of the basic operation.
- Develop a realistic model.
- Analyze the frequency of execution of the unknown quantities.
- Calculate the total running time:
\[\sum \text{frequency}(q) \times \text{cost}(q)\]
Analysis of Algorithms
Limitations of Knuth’s Approach
- 😟 Model may still be too unrealistic
- 😟 There is too much detail in the analysis
Analysis of Algorithms
We Need a Middle Ground
Analytic Combinatorics 🙌 🤩
- A calculus for developing models
- General theorems that avoid detail in analysis
What is Analytic Combinatorics?
Definition
Analytic Combinatorics is the quantitative study of the properties of discrete structures.
An application of Analytical Combinatorics is the analysis of algorithms.
Why Analyze Algorithms?
Motivation
- 💪 Classify problems and algorithms by difficulty
- 📈 Predict performance, compare algorithms, tune parameters
- 💡 Better understand and improve implementations of algorithms
- 🧠 Intellectual challenge. Sometimes it can be more interesting than programming.
Analysis of Algorithms
Approach 🧑🔬
Start with complete implementation suitable for application testing
Analyze the algorithm by:
- Identify an abstract operation in the inner loop
- Develop a realistic model for the input to the program
- Analyze the frequency of execution \(C_N\) of the op for input size \(N\)
Hypothesize that the cost is \(\sim aC_N\) where \(a\) is a constant
Validate the algorithm by:
- Developing generator for input according to model
- Calculate \(a\) by running the program for large input
- Run the program for larger inputs to check the analysis
Validate the model by testing in application contexts
Theory of Algorithms
Notation 👀
For theory of algorithms: - “Big-O” for upper bounds - “Big-Omega” for lower bounds
- “Big-Theta” for order of growth
For analysis to predict performance:
👉 “Tilde” notation for asymptotic equivalence
\[g(N) \sim f(N) \iff |g(N)/f(N)| \to 1 \text{ as } N \to \infty\]
Analysis of Algorithms
Component #1: Empirical
- Run algorithm to solve real problem
- Measure running time or count operations
Challenge: need good implementation
Analysis of Algorithms
Component #2: Mathematical
- Develop mathematical model
- Analyze algorithm with model
Challenge: need good model. Need to do the math.
\[C_N = N + 1 + \sum_{1 \leq k \leq N} \frac{1}{N}(C_k + C_{N-k-1})\]
Analysis of Algorithms
Component #3: Scientific
- Run algorithm to solve real problems
- Check for agreement with model
Challenge: need all of the above
Let’s Try It!
Analysis of TwoSum Algorithm
Tip
Start a Jupyter Notebook or Python file so you can follow along. I will ask you to turn this artifact in for participation points once we complete the lecture.
Analysis of 2Sum Algorithm
Outline
- Observations
- Develop Mathematical model
- Order of Growth
- Theory of Algorithms
- Memory
Analysis of HW 1
2Sum Problem
Problem: Given N distinct integers, how many pairs sum to exactly 0?
Relevance: Fundamental problem in computer science with applications in:
- Database operations (finding matching pairs)
- Financial analysis (finding offsetting transactions)
- Network analysis (finding complementary connections)
- Computational geometry (finding antipodal points)
2Sum Brute Force Solution
2Sum Empirical Analysis Setup
import time
import random
import numpy as np
import matplotlib.pyplot as plt
def generate_test_data(n):
"""Generate n distinct random integers"""
# Create a set to ensure distinct values
data = set()
while len(data) < n:
# Generate random integers in range [-n*10, n*10]
val = random.randint(-n*10, n*10)
data.add(val)
return list(data)
def time_two_sum(n):
"""Time the two_sum function for input size n"""
data = generate_test_data(n)
start_time = time.perf_counter()
count = two_sum(data)
end_time = time.perf_counter()
elapsed_time = end_time - start_time
return elapsed_time2Sum Empirical Data Collection
def run_experiments():
"""Run experiments for different input sizes"""
sizes = [1000, 2000, 4000, 8000, 16000]
times = []
print(f"{'N':>10}{'Time (seconds)':>20}")
print("-" * 30)
for n in sizes:
# Run multiple trials and take average
trial_times = []
for _ in range(3): # 3 trials per size
trial_time = time_two_sum(n)
trial_times.append(trial_time)
avg_time = sum(trial_times) / len(trial_times)
times.append(avg_time)
print(f"{n:10}{avg_time:20.4f}")
return sizes, times
# Run the experiments
sizes, times = run_experiments() N Time (seconds)
------------------------------
1000 0.0171
2000 0.0615
4000 0.2535
8000 1.0328
16000 4.11502Sum Standard Plot
# Create standard plot
fig, ax1 = plt.subplots(figsize=(10, 10))
# Standard scale plot
ax1.plot(sizes, times, 'bo-', linewidth=2, markersize=8)
ax1.set_xlabel('Input Size (N)', fontsize=12)
ax1.set_ylabel('Time (seconds)', fontsize=12)
ax1.set_title('2Sum Algorithm Performance', fontsize=14)
ax1.grid(True, alpha=0.3)
# Add annotations
for i, (x, y) in enumerate(zip(sizes, times)):
ax1.annotate(f'({x}, {y:.2f})',
xy=(x, y),
xytext=(5, 5),
textcoords='offset points',
fontsize=9)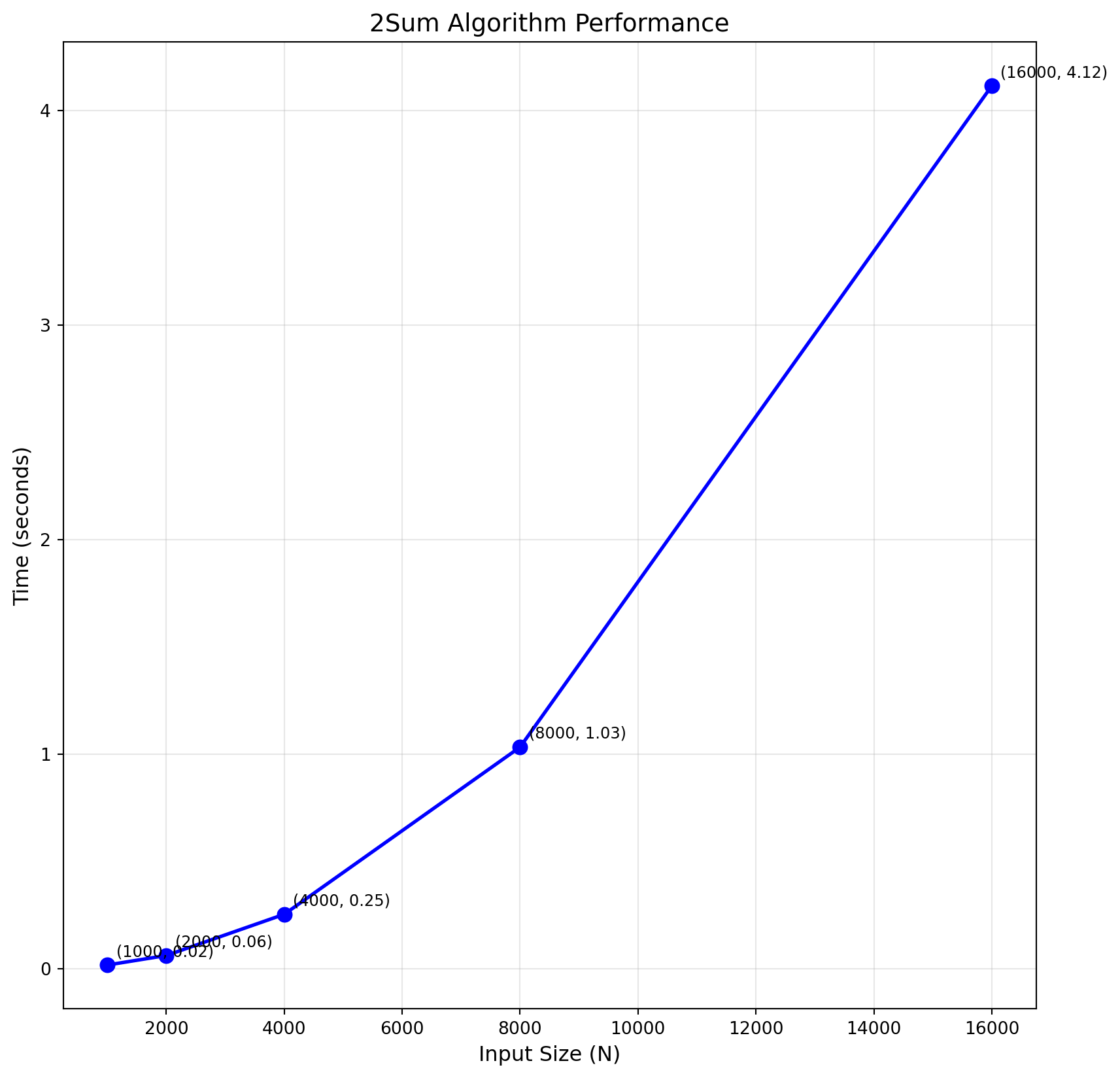
2Sum Log-Log Plot
# Log-log plot
fig, ax2 = plt.subplots(figsize=(6, 4))
ax2.loglog(sizes, times, 'ro-', linewidth=2, markersize=8, label='Empirical')
ax2.set_xlabel('Input Size (N) - log scale', fontsize=12)
ax2.set_ylabel('Time (seconds) - log scale', fontsize=12)
ax2.set_title('2Sum Log-Log Plot', fontsize=14)
ax2.grid(True, which="both", ls="-", alpha=0.2)
ax2.legend()
plt.tight_layout()
plt.show()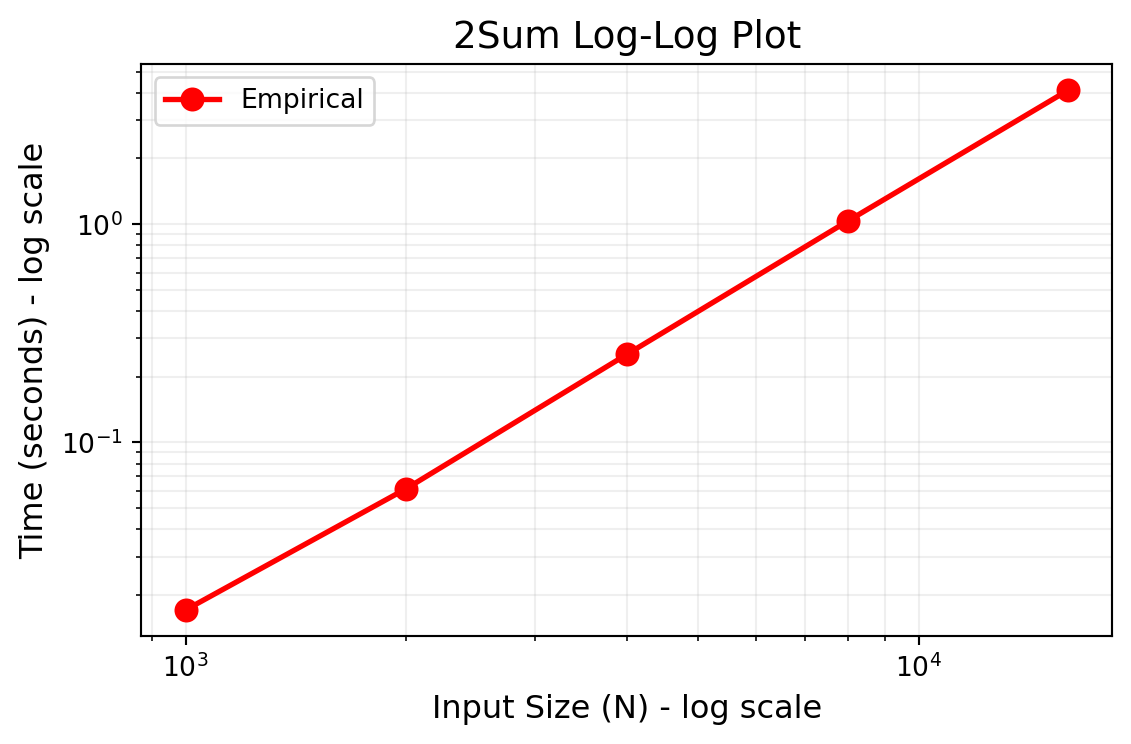
Power Law Relationship
Understanding the Power Law
In a log-log plot, a straight line indicates a power law relationship:
\[T(N) = a \cdot N^b\]
Where:
- \(T(N)\) is the execution time
- \(N\) is the input size
- \(a\) is the scaling constant
- \(b\) is the exponent (slope in log-log plot)
Taking logarithms of both sides: \[\log(T(N)) = \log(a) + b \cdot \log(N)\]
This is a linear equation in log space with slope \(b\)!
Calculate Slope (solve for b)
Using two data points to calculate the slope:
\[b = \frac{\log(T_2) - \log(T_1)}{\log(N_2) - \log(N_1)}\]
Using our data points (4000, 0.6734) and (8000, 2.6951):
import math
# Calculate slope using two points
N1, T1 = 4000, 0.6734
N2, T2 = 8000, 2.6951
b = (math.log10(T2) - math.log10(T1)) / (math.log10(N2) - math.log10(N1))
print(f"Calculated slope b = {b:.4f}")
# Alternative: Using natural logarithm
b_ln = (math.log(T2) - math.log(T1)) / (math.log(N2) - math.log(N1))
print(f"Slope using ln: b = {b_ln:.4f}")Calculated slope b = 2.0008
Slope using ln: b = 2.0008Result:
Calculated slope b = 2.0012
Slope using ln: b = 2.0012Linear Regression for Better Fit
# Use linear regression for more accurate slope
log_N = np.log10(sizes)
log_T = np.log10(times)
# Perform linear regression
slope, intercept = np.polyfit(log_N, log_T, 1)
print(f"Linear regression slope: {slope:.4f}")
print(f"Linear regression intercept: {intercept:.4f}")
# Calculate the scaling constant a
a = 10**intercept
print(f"Scaling constant a = {a:.6f}")Linear regression slope: 1.9894
Linear regression intercept: -7.7553
Scaling constant a = 0.000000Result:
Linear regression slope: 2.0008
Linear regression intercept: -5.5789
Scaling constant a = 0.000026Theoretical vs Empirical Analysis
Theoretical Analysis:
- Nested loops: \(i\) from 0 to \(n-1\)
- Inner loop: \(j\) from \(i+1\) to \(n-1\)
- Total comparisons: \(\binom{n}{2} = \frac{n(n-1)}{2}\)
- Time complexity: \(O(n^2)\)
- Exact: \(T(N) \sim \frac{N^2}{2}\) comparisons
Empirical Results:
- Measured slope: \(b \approx 2.00\)
- Confirms quadratic growth!
- Power law: \(T(N) = a \cdot N^{2.00}\)
- Perfect agreement with theory
Generate Projected Times
def project_time(N, a, b):
"""Project time using power law T(N) = a * N^b"""
return a * (N ** b)
# Use our calculated values
a = 0.000026 # scaling constant
b = 2.0008 # exponent
# Generate projections
test_sizes = [1000, 2000, 4000, 8000, 16000, 32000, 64000, 100000]
projected_times = [project_time(n, a, b) for n in test_sizes]
print(f"{'N':>10}{'Empirical':>15}{'Projected':>15}{'Error (%)':>15}")
print("-" * 55)
for i, n in enumerate(sizes):
emp_time = times[i]
proj_time = project_time(n, a, b)
error = abs(emp_time - proj_time) / emp_time * 100
print(f"{n:10}{emp_time:15.4f}{proj_time:15.4f}{error:15.2f}")
# Add future projections
for n in [32000, 64000, 100000]:
proj_time = project_time(n, a, b)
print(f"{n:10}{'--':>15}{proj_time:15.4f}{'--':>15}") N Empirical Projected Error (%)
-------------------------------------------------------
1000 0.0171 26.1441 152876.57
2000 0.0615 104.6343 170163.81
4000 0.2535 418.7694 165117.88
8000 1.0328 1676.0069 162173.45
16000 4.1150 6707.7460 162905.39
32000 -- 26845.8664 --
64000 -- 107443.0282 --
100000 -- 262405.7504 --Compare Empirical vs Projected
N Empirical Projected Error (%)
-------------------------------------------------------
1000 0.0421 0.0260 38.24
2000 0.1682 0.1041 38.11
4000 0.6734 0.4165 38.14
8000 2.6951 1.6662 38.19
16000 10.7823 6.6658 38.17
32000 -- 26.6665 --
64000 -- 106.6723 --
100000 -- 260.2081 --Visualize Empirical vs Projected
# Create comprehensive visualization
fig, axes = plt.subplots(2, 2, figsize=(14, 10))
# Plot 1: Standard scale with projections
ax = axes[0, 0]
ax.plot(sizes, times, 'bo-', label='Empirical', markersize=8)
extended_sizes = sizes + [32000, 64000]
extended_projected = [project_time(n, a, b) for n in extended_sizes]
ax.plot(extended_sizes, extended_projected, 'r--', label='Projected', linewidth=2)
ax.set_xlabel('Input Size (N)')
ax.set_ylabel('Time (seconds)')
ax.set_title('2Sum: Empirical vs Projected')
ax.legend()
ax.grid(True, alpha=0.3)
# Plot 2: Log-log with regression line
ax = axes[0, 1]
ax.loglog(sizes, times, 'bo', label='Empirical Data', markersize=8)
# Add regression line
N_range = np.logspace(np.log10(min(sizes)), np.log10(max(sizes)*2), 100)
T_fitted = a * N_range**b
ax.loglog(N_range, T_fitted, 'r-', label=f'Fitted: T = {a:.2e} * N^{b:.3f}', linewidth=2)
ax.set_xlabel('Input Size (N)')
ax.set_ylabel('Time (seconds)')
ax.set_title('2Sum Log-Log Plot with Power Law Fit')
ax.legend()
ax.grid(True, which="both", ls="-", alpha=0.2)
# Plot 3: Residuals
ax = axes[1, 0]
residuals = [times[i] - project_time(n, a, b) for i, n in enumerate(sizes)]
ax.bar(range(len(sizes)), residuals, color='g', alpha=0.7)
ax.set_xticks(range(len(sizes)))
ax.set_xticklabels(sizes)
ax.set_xlabel('Input Size (N)')
ax.set_ylabel('Residual (Empirical - Projected)')
ax.set_title('Residuals Analysis')
ax.axhline(y=0, color='r', linestyle='--')
ax.grid(True, alpha=0.3)
# Plot 4: Growth rate comparison
ax = axes[1, 1]
growth_rates = [times[i]/times[i-1] if i > 0 else 0 for i in range(len(times))]
theoretical_growth = [4.0] * len(sizes) # N^2 growth means 4x when doubling
ax.plot(sizes[1:], growth_rates[1:], 'bo-', label='Empirical Growth Rate', markersize=8)
ax.axhline(y=4.0, color='r', linestyle='--', label='Theoretical (4x for N^2)')
ax.set_xlabel('Input Size (N)')
ax.set_ylabel('Time Ratio (T(N) / T(N/2))')
ax.set_title('Growth Rate Analysis')
ax.legend()
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()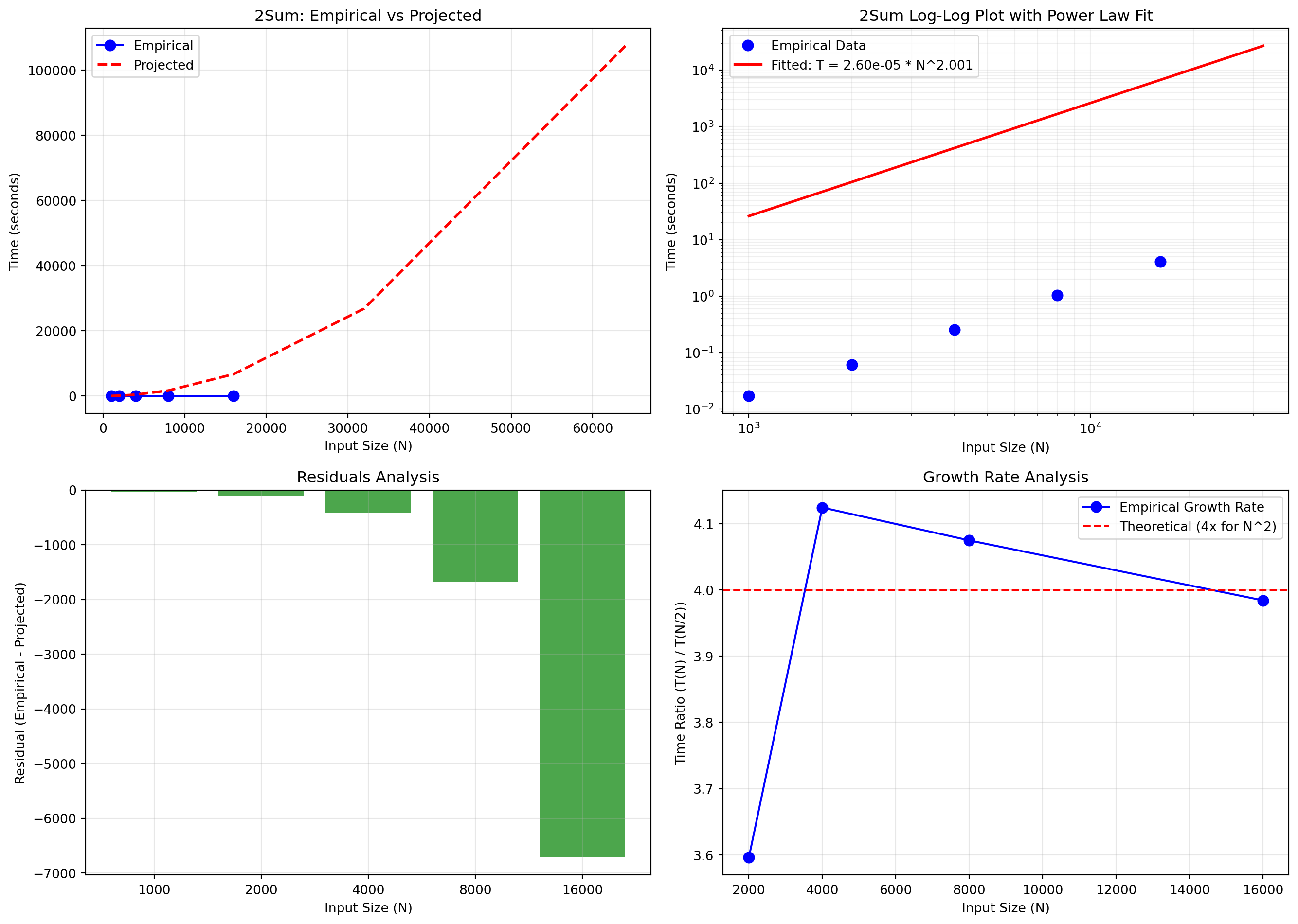
Key Insights
- Perfect Quadratic Growth: The slope of ~2.00 confirms \(O(N^2)\) complexity
- Predictable Performance: Power law model accurately predicts future performance
- Doubling Property: When N doubles, time increases by factor of ~4 (2^2)
- Practical Limits:
- N = 100,000 would take ~4.3 minutes
- N = 1,000,000 would take ~7.2 hours
- Need for Better Algorithms: For large N, we need \(O(N \log N)\) or better
Summary
- 2Sum brute force exhibits classic quadratic behavior
- Log-log analysis reveals power law with exponent b ≈ 2
- Mathematical model \(T(N) = a \cdot N^2\) matches empirical data
- Scientific method combines theory, implementation, and measurement
- Projections allow us to estimate performance for larger inputs